Kurzwellige Strahlung: Unterschied zwischen den Versionen
energie>WikiSysop |
energie>WikiSysop |
||
| Zeile 25: | Zeile 25: | ||
Mit dem Tag des Jahres als Winkel (<code>J' = J*36°/360</code>) lässt sich dann die Zeitgleichung | Mit dem Tag des Jahres als Winkel (<code>J' = J*36°/360</code>) lässt sich dann die Zeitgleichung | ||
Zgl(J) = 0,0066 + 7,3525*cos(J'+85,9°) + 9,9359*cos(2*J'+108,9°) + 0,3387*cos(3*J'+105,2°) | Zgl(J) = 0,0066 + 7,3525*cos(J'+85,9°) + 9,9359*cos(2*J'+108,9°) + 0,3387*cos(3*J'+105,2°) | ||
, der Stundenwinkel ω | |||
ω = | |||
und die Sonnendeklination | und die Sonnendeklination | ||
δ(J) = 0,3948 - 23,2559*cos(J'+9,1°) - 0,3915*cos(2*J'+5,4°) - 0,1764*cos(3*J'+26,0°) | δ(J) = 0,3948 - 23,2559*cos(J'+9,1°) - 0,3915*cos(2*J'+5,4°) - 0,1764*cos(3*J'+26,0°) | ||
ermitteln. | ermitteln. | ||
Die '''Sonnenhöhe γ<sub>S</sub>''' ermittelt sich aus der Lage des Ortes (φ = Breitengrad [Latitude]), dem Stundenwinkel ω und der Deklination: | Die '''Sonnenhöhe γ<sub>S</sub>''' ermittelt sich aus der Lage des Ortes (φ = Breitengrad [Latitude]), dem Stundenwinkel ω und der Deklination: | ||
Version vom 12. Januar 2018, 02:39 Uhr
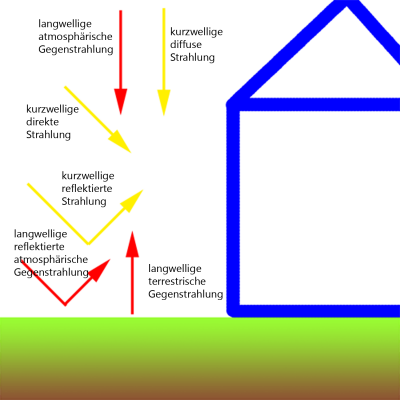
Kurzwellige Strahlung (direkte, diffuse und reflektierte Solarstrahlung = solare Wärmeeinträge)
Kurzwellige Strahlung (mit Wellenlängen von ca. 0.5 - 1 µm => sichtbarer Lichtbereich 380-780 nm) stammt von der Sonne, erreicht Werte bis ca. 1000 W/m² und weist einen ausgeprägten Tagesgang auf. Nachts ist keine kurzwellige Strahlung vorhanden. Bauteile können kurzwellige Strahlung absorbieren und reflektieren aber nicht selbst aussenden.
- kurzwellige diffuse Strahlung
- kurzwellige direkte Strahlung
- kurzwellige Globalstrahlung (Summe aus direkter und indirekter Strahlung)
- kurzwellige reflektierte Strahlung
Die kurwellige direkte Strahlung wird meist als Strahlung auf einer ebenen (horizontalen) Fläche gemessen. Für die Berücksichtigung in der Berechnung muss der Sonnenstand und die Ausrichtung des Bauteils berücksichtigt werden.
Berechnungen
mittlere Ortszeit, wahre Ortszeit, Stundenwinkel
Für die kurzwellige Strahlung ist es wichtig, den Standort und die Strahlungsrichtung der Sonne zu kennen. Für die Berechnung des Sonnenstandes ist deshalb der Standort entscheidend. Daraus ermittelt sich die mittlere Ortszeit (MOZ) und die wahre Ortszeit (WOZ):
MOZ = ... WOZ = ...
Der Stundenwinkel ω ist die Zeit des Tages als Winkel:
ω = ...
Zeitgleichung, Sonnendeklination, Sonnenhöhe, Azimut
Mit dem Tag des Jahres als Winkel (J' = J*36°/360) lässt sich dann die Zeitgleichung
Zgl(J) = 0,0066 + 7,3525*cos(J'+85,9°) + 9,9359*cos(2*J'+108,9°) + 0,3387*cos(3*J'+105,2°)
, der Stundenwinkel ω
ω =
und die Sonnendeklination
δ(J) = 0,3948 - 23,2559*cos(J'+9,1°) - 0,3915*cos(2*J'+5,4°) - 0,1764*cos(3*J'+26,0°)
ermitteln.
Die Sonnenhöhe γS ermittelt sich aus der Lage des Ortes (φ = Breitengrad [Latitude]), dem Stundenwinkel ω und der Deklination:
γS = arcsin( cos ω * cos φ * cos δ + sind φ * sin δ )
Mit der Sonnenhöhe lässt sich auch das Azimut (Horizontalwinkel) der Sonne berechnen:
αS = ...
Strahlungswerte
Die mittlere extraterrestrische Solarstrahlung beträgt etwa I0,mittel = 1.367 W/m². Die vom Sonnenabstand abhängige extraterrestrische Strahlung kann wie folgt ermittelt werden: I0 = I0,mittel * 1 + 0,03344 * cos(J').
Die auf der Erde auftreffende kurzwellige Strahlung ist von der Raylight Atmosphäre δR0 und der Dicke der mittleren Luftmasse sowie der geografischen Höhe (Luftdruck) abhängig.
Umrechnung auf beliebige Orientierungen
...
Berechnungen der kurzwelligen Strahlung des unbedeckten Himmels (Clear Sky Model)
- ASHARE Clear Sky model (Ashare Clear Sky Model, 2005) -> siehe EnergyPlus
- ASHARE Clear Sky model (Ashare Revised Clear Sky Model, 2009) -> siehe EnergyPlus
- Zhang-Huang Solar Model -> siehe EnergyPlus
- Perez Direkt/Diffuse Splitting Model -> siehe EnergyPlus
- VDI 6007 / VDI ...
- NREL Eugene L. Maxwell: Clear Sky Model, 1987
- NREL Richard E. Bird / Roland L. Hulstrom: A Simplified Clear Sky Model, 1981
