Kelvin-Gleichung: Unterschied zwischen den Versionen
energie>WikiSysop Änderung 27760 von WikiSysop (Diskussion) rückgängig gemacht. |
Keine Bearbeitungszusammenfassung |
||
| (21 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigationsleiste Feuchteschutz}} | {{Navigationsleiste Feuchteschutz}} | ||
Mit der Kelvingleichung lässt sich die [[Feuchtespeicherfunktion]] zwischen Sorptionskurve und Saugspannungskurve umrechnen. Zu diesem Zweck wird die Temperatur der Umrechnung auf 20°C festgelegt. Mit der Kelvingleichung lässt sich der Kapillardruck p<sub>c</sub> für eine relative Luftfeuchte ermitteln. | Mit der Kelvingleichung lässt sich die [[Feuchtespeicherfunktion]] zwischen Sorptionskurve und Saugspannungskurve umrechnen. Zu diesem Zweck wird die Temperatur der Umrechnung auf 20°C festgelegt. Mit der Kelvingleichung lässt sich der [[Saugdruck]] (bzw. Kapillardruck) p<sub>c</sub> für eine relative Luftfeuchte ermitteln. | ||
< | [[Datei:Kelvingleichung.png|right|400px]] | ||
:<math>p_c=-\rho_w \cdot R_v \cdot T_{ref} \cdot ln{(\varphi)}</math> | |||
:<math>\varphi = \exp{(\frac{-p_c}{\rho_w \cdot R_v \cdot T_{ref}})}</math> | |||
* p<sub>c</sub> = Kapillardruck [Pa] | |||
* ρ<sub>w</sub> = 1000 kg/m³ Flüssigwasserdichte | * ρ<sub>w</sub> = 1000 kg/m³ Flüssigwasserdichte | ||
* R<sub>v</sub> = 462 J/(kgK) Gaskonstante für Wasserdampf | * R<sub>v</sub> = 462 J/(kgK) [[Spezifische Gaskonstante]] für Wasserdampf | ||
* T<sub>ref</sub> = 293,15 K Thermodynamische Temperatur bei 20°C | * T<sub>ref</sub> = 293,15 K Thermodynamische Temperatur bei 20°C | ||
* φ = relative Luftfeuchte 0..1 | * φ = [[Luftfeuchtigkeit|relative Luftfeuchte]] 0..1 | ||
Für eine relative Luftfeuchte von über 100% (wie sie im Rechenmodell von WUFI verwendet wird) ist die zwar definiert. Die Umrechnung in Delphin wird aber über den Logarithmus des Drucks definiert. Da bei Werten über 100% jedoch ein negativer Druck entsteht, ist dieser als Logarithmus in den Funktionsgleichungen nicht mehr darstellbar. Für 0% relative Luftfeuchte ist die Kelvinfunktion nicht anwendbar. Für diesen Fall wird mit einem vergleichbar hohen Kapillardruck (z.B. 1e10 Pa) gerechnet. | |||
Die Gleichung basiert auf den Gleichgewichtsbedingungen nach Kelvin-Thomson in Verbindung mit dem [[Porenmodell]]: | |||
:<math>\varphi = exp \left[- \frac{2 \cdot \sigma \cdot cos \theta}{r \cdot \rho_w \cdot R_v \cdot T} \right]</math> | |||
:<math>p_c = \frac{2 \cdot \sigma \cdot cos \theta}{r}</math> | |||
* σ = Oberflächenspannung des Wassers [N/m] | |||
* θ = Randwinkel [°] | |||
* r = Kapillarradius | |||
* ρ<sub>w</sub> = 1.000 kg/m³ Rohdichte Wasser | |||
{{siehe auch|[[Feuchtespeicherfunktion]], [[wikipedia:de:Kelvingleichung]]}} | {{siehe auch|[[Feuchtespeicherfunktion]], [[wikipedia:de:Kelvingleichung]], [[Luftfeuchtigkeit]], [[Sättigungsdampfdruck]], [[Porenmodell]], [[Saugdruck]]}} | ||
[[Kategorie: Feuchteschutz]] | [[Kategorie: Feuchteschutz]] | ||
Aktuelle Version vom 12. Oktober 2023, 12:39 Uhr
Mit der Kelvingleichung lässt sich die Feuchtespeicherfunktion zwischen Sorptionskurve und Saugspannungskurve umrechnen. Zu diesem Zweck wird die Temperatur der Umrechnung auf 20°C festgelegt. Mit der Kelvingleichung lässt sich der Saugdruck (bzw. Kapillardruck) pc für eine relative Luftfeuchte ermitteln.
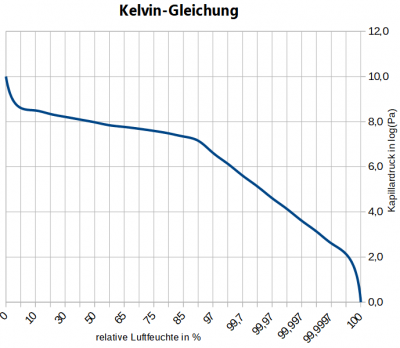
- [math]\displaystyle{ p_c=-\rho_w \cdot R_v \cdot T_{ref} \cdot ln{(\varphi)} }[/math]
- [math]\displaystyle{ \varphi = \exp{(\frac{-p_c}{\rho_w \cdot R_v \cdot T_{ref}})} }[/math]
- pc = Kapillardruck [Pa]
- ρw = 1000 kg/m³ Flüssigwasserdichte
- Rv = 462 J/(kgK) Spezifische Gaskonstante für Wasserdampf
- Tref = 293,15 K Thermodynamische Temperatur bei 20°C
- φ = relative Luftfeuchte 0..1
Für eine relative Luftfeuchte von über 100% (wie sie im Rechenmodell von WUFI verwendet wird) ist die zwar definiert. Die Umrechnung in Delphin wird aber über den Logarithmus des Drucks definiert. Da bei Werten über 100% jedoch ein negativer Druck entsteht, ist dieser als Logarithmus in den Funktionsgleichungen nicht mehr darstellbar. Für 0% relative Luftfeuchte ist die Kelvinfunktion nicht anwendbar. Für diesen Fall wird mit einem vergleichbar hohen Kapillardruck (z.B. 1e10 Pa) gerechnet.
Die Gleichung basiert auf den Gleichgewichtsbedingungen nach Kelvin-Thomson in Verbindung mit dem Porenmodell:
- [math]\displaystyle{ \varphi = exp \left[- \frac{2 \cdot \sigma \cdot cos \theta}{r \cdot \rho_w \cdot R_v \cdot T} \right] }[/math]
- [math]\displaystyle{ p_c = \frac{2 \cdot \sigma \cdot cos \theta}{r} }[/math]
- σ = Oberflächenspannung des Wassers [N/m]
- θ = Randwinkel [°]
- r = Kapillarradius
- ρw = 1.000 kg/m³ Rohdichte Wasser
